大学で学ぶ数学の内容はどんなもの？！

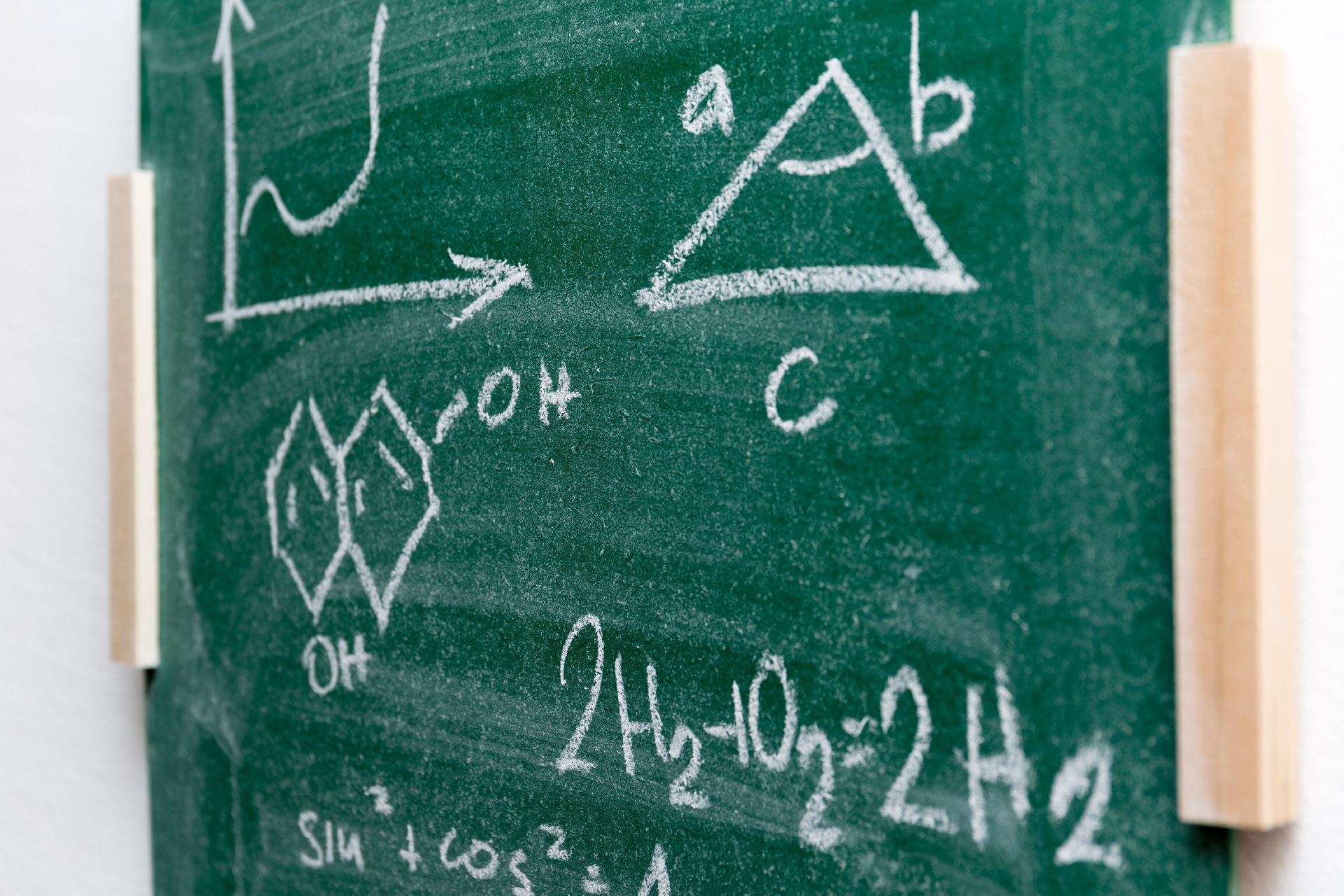
高校までの数学と違って大学ではどんなことを学ぶのでしょうか？大学を選ぶときにも参考になると思ったので参考になりそうな内容をまとめてみました。

スポンサーリンク

スポンサーリンク

大学で学ぶ数学の内容は“数”の基礎研究

他分野の発展にも貢献する“数”の基礎研究
数学は代数学、幾何学、解析学の三つに大きく分けることができます。「代数学」では、方程式の文字の種類を増やした多元方程式や“数学の女王”といわれる整数論を研究しています。「幾何学」は、高校で学ぶ微分法を踏まえた微分幾何学と、位相幾何学と呼ばれている“トポロジー”を研究しています。「解析学」は微分・積分の延長線上にあり、物理学の力学や電磁気学と密接な関係があります。また近年、コンピュータに象徴される“応用数学”も注目されています。

現在の数学で特徴的なのはトポロジーの概念で、これは三角形と円を同じものと見なす一見不思議な概念です。しかしこれは物事の本質を見極めるうえで大変役立つ思考法となっていて、数学以外の分野にも取り入れられています。例えば、医学では心臓病による死が、このトポロジーの考え方で説明されることがあるのです。

また最近では、数理物理と呼ばれる領域がめだっています。トポロジーや代数・幾何、解析などの分野を幅広く活用し、理論物理学を展開します。数学と物理学との相互乗り入れにより、新しい学問分野を開いているのです。

引用元-数学 │ 学問・大学情報 ｜ Benesse マナビジョン

大学で勉強した数学の内容よありも「みにつけられた論理的な力」が強みになる！！

数学科の卒業生が世の中に出た場合、他学科の卒業生に対して何が一体強みな のでしょう？私は「論理的に書かれたテキストを論理的に読みこなす力がある こと」だと思います。正直言って、大学で学んだ数学が世の中に出て役に立つ ことなんて滅多にありません。そりゃあ、ファイナンス数学を勉強すれば金融 関係の仕事で、整数論を勉強すれば暗号関係の仕事で何らかの役には立つでしょ うし、中学や高校の教師になれば、大学で勉強した事が全て役に立つ、と言え るかも知れません。でも、誰もが証券会社で年がら年中伊藤の公式をいじっ て数値解析のプログラムをブン回して、という仕事に就くわけでもなし、誰も が暗号技術者になるわけでもなし、中学や高校の教師が数学だけ教えていれば 良いわけでもない。暗号関係をのぞく情報関連に進んだ場合は、数学を使う仕 事なんてほとんど無いでしょう。あったとしても、たいていはあまり重要でな い局面に限られていますから、数学的な部分はゴマカシて前に進むのです。私 なんぞは、たまたま一時期特殊な研究所に勤めていたから、数理論理学だ けは使いましたが、微分も積分も行列もきれいさっぱり忘れて、 ただただ楽しく(？)毎日を過ごしておりました。

大学で勉強した数学の内容よりも、数学を勉強することによって身に付けられ た「論理的に書かれたテキストを論理的に読みこなす力」の方がうんと普遍的 で、何処に行っても役に立つと思います。

引用元-

大学物理の内容と必要な数学の分野

理学系・工学系の学部では主に大学1、2年で古典物理学の基礎的なことを学びます。

・古典力学：微分方程式
→運動方程式は二階の微分方程式です。質点だけでなく大きさを持った剛体も扱います。慣性モーメントなどを計算する際には面積分や体積積分が必要になります。

・古典電磁気学：ベクトル解析，微分方程式
→静電場，静磁場，電場と磁場の相互作用などを学びます。電磁気学の基本法則を記述するのに必要なベクトル解析で多くの人が苦戦します。マクスウェル方程式は偏微分方程式です。力学よりも必要とされる数学がやや高度。

・熱力学：偏微分
→エントロピーとか学びます。熱力学の基礎的な部分はあまり高度な数学を必要としませんが，偏微分に慣れておく必要があります。

・振動・波動論：フーリエ解析
→弦や質点の振動を扱います。フーリエ級数展開，フーリエ変換という道具を使います。

・解析力学：変分法
→ニュートンの運動方程式を変分法を用いて言い換えると解析力学の基本方程式であるオイラーラグランジュ方程式となります。

・流体力学：偏微分方程式，数値解析
→ナビエ・ストークス方程式は偏微分方程式。流体力学ではシミュレーション（数値実験）が重要。

・特殊相対性理論
→ローレンツ変換，光速度不変の原理など。非常に面白い上に高度な数学は必要としません。しかし，古典力学と異なり直感に反するので理解するのは簡単ではありません。

・一般相対性理論：非ユークリッド幾何学
→曲がった空間を扱うための幾何学が必要になります。

引用元-大学物理の内容と必要な数学の分野 | 高校数学の美しい物語

大学数学で学ぶ具体的な内容例

私の通っていた大学（数学科）の場合を必修を中心に紹介します。大学が違えばまたちがうと思います。

まず1年で線形代数と微分積分を習います。ここは比較的高校時代とのつながりがあるのでみんなついてきます。
線形代数は高校の時に習った行列の続きのようなもの（大学では3次以上の行列も扱うんですが）、微分積分は多変数の微分積分（重積分と言って、∫ がいくつも出てきます）をやったりします。イプシロンデルタ論法という、少しやっかいなものを習います。これは高校までは何となく直感でやっていた収束や極限などの概念を厳密に言いなおしたものです。

２年生になると代数で群論という授業が始まります。現代数学のすべての分野で現れますので、これは必修です。私は群というものの概念がこれまでの数学とは違って独特で、把握するのに結構苦労した記憶があります。
さらに集合と位相。これは前半の集合論はまだ分かりやすいのですが、後半の位相空間論になると抽象的になってきますので難しくて投げ出す人も多く出てきます。
解析学序論。1年のときに習った微分積分のさらに続きのようなものです。ベクトル解析など物理への応用もできるものをやります。

引用元-大学数学で学ぶ内容について – 具体的にどのよう… – 高校数学 | Yahoo!知恵袋

大学で学ぶ実用数学の内容とは？

「実用数学」と書くと高校生の中には「数学なんて使わなくても実生活では困らない。」と言う人もいるかもしれない。確かに私生活では算数だけでじゅうぶんだし、大人になって社会に出たとしても数学を使わずにできる仕事はいくらでもある。

けれどもこの世界がカネとモノと人で動いていることは明らかな事実だ。だからカネとモノと人の量の変化を分析し、将来の予測や判断に活かして仕事を効率的に進めたいと思うならば数学は不可欠で、強力なツールとなる。

将来、技術系や工学系、化学系、金融系、製薬業界、保険業界の仕事に就くのならもちろん数学は必要だし、売上分析のための統計解析はどの分野の企業でも必要とされる数学だ。

要は生き方のスタイルの違いなのだと思う。自分の感性や感覚だけをたよりに生きるか、それともそれに数学的な分析を加えて生きるか。どちらを自分が選択をするかということなのだ。

今日紹介する範囲の「実用数学」はこうした意味で「つぶしの効く」知識であり、身につけることができれば応用範囲は広い。学んでおいて損はない。

引用元-大学で学ぶ数学とは（実用数学編） – とね日記

まとめ

私は大学ではほとんど数学は学ばなかったのですが論理的な内容を学ぶことでその力が社会に出てから役に立つのですね。複雑な計算式などを覚えることが大変そうというイメージがありましたが、実用的なところを知ると励みになりそうです。

twitterの反応

最近大型書店の数学書コーナー行くと年配の人で数人で来てて「この本何処何処迄読んだけど◯◯が分からなくて挫折した。教えてくれる塾とかあればいいのに…」と話し合ってる方々を度々見かける。多分、数学塾(大学以上の内容)は結構需要があると思った。

— 原子心母 (@atomotheart) March 15, 2016

4月下旬『朝倉　数学辞典』川又雄二郎他編　21600円（朝倉書店）
大学学部生から大学院生を対象に調べたい項目を読めば理解できるよう配慮したわかりやすい数学辞典。高校程度から専門分野の内容までの諸分野を各2～3ページ程度で五十音順に配列、数式は最小限にとどめ、図を用いて平易に解説

— 書泉_MATH (@rikoushonotana) March 13, 2016

大学の数学とか物理オタの人達って数学ガールの内容は常識になっているんだろうか

— 由条仁史 (@maathyiyi) March 15, 2016

伝左衛門さんの「大学への数学」のツイートを見かけた気がするが、私は現代数学社の方が好きだった。受験数学の傾向など全く無視して独自路線を行く孤高な感じが好き。東京出版の方は何か、進学校のエリート雑誌という感じで嫌いだった。（ただし内容は良い。）

— Ryo (@awtjvyjz) March 15, 2016

本日、3月17日（木）１３：３０～大学受験科（高卒生コース）の入学説明会を実施いたします。
１４：３０～は数学の体験授業も行います。本日は私立大・センター対策の内容です。お友達とお誘い合わせのうえ、ぜひご来校ください♪

— 代ゼミ大阪南校 (@yozemi_osaka) March 17, 2016

Q.編入試験と浪人ってどっちの方が大変?
A.編入試験は国公立大でも科目数が少ないので数の負担は少ないです。ただし、試験問題は大学の内容になるので数学や物理は結局高校の基礎が重要で、そこに+αが必要になってきます。また、周りが学生生活を謳歌している中で誘いを断っての受験生活は精神

— 理系大学編入支援(bot) (@science_hennnyu) March 17, 2016

https://twitter.com/mryshohgk/status/710724234385821696
https://twitter.com/feynman_M6Bap/status/710820036177371136

【数学の勉強法】

・『計算』は必ず【自分の手】でする

・解法を丸暗記しない

・単元ごとの《解法のリンク》を常に意識

・『一つ上のレベルの大学』に勉強内容を合わせる

・『二次試験レベル』の勉強を【第一優先】に

・『教科書レベル・センター基礎レベル』はまとめて《2ヶ月》で

— 現役国立合格への【最短距離】勉強法 (@kkdr_saitan) March 18, 2016

大学の教科書って内容が飛んでるところが多い
書かなくても解るよねって気持ちが伝わってくるが
肝心な内容は理解し辛い,数学の教科書で途中の式ふっ飛ばして
結論を書くから行間を理解するのに一苦労

— muchi (@muchi_00) March 19, 2016

“